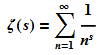UNSOLVED PROBLEMS

In Number Theory, Logic, and Cryptography

Riemann Hypothesis

 

The Riemann Hypothesis only just qualifies for these pages, as a greater level of mathematical sophistication is required for its understanding than for the other problems on this site.  The Clay Mathematics Institute is offering a prize of $1,000,000 for a valid proof.

The Riemann zeta-function ζ(s) is a function of a complex variable s defined by :

 

 

 

using analytical continuation for all complex s ≠ 1.  The Riemann Hypothesis states that all of the non-trivial zeroes of this function lie on a vertical straight line with real part equal to exactly 1/2.

The problem is to prove the hypothesis, or find a counter-example..

 

For further information, please see:

[1] http://mathworld.wolfram.com/RiemannHypothesis.html

[2] http://www.claymath.org/millennium/Riemann_Hypothesis/

[3] http://en.wikipedia.org/wiki/Riemann_hypothesis

 

You can check for contributions to this problem on the solutions page.

 

——————————–-

This web site developed and maintained by

Tim S Roberts

Email: timro21@gmail.com