UNSOLVED PROBLEMS

In Number Theory, Logic, and Cryptography

4D Euler Brick

 

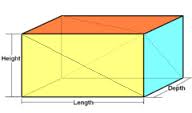
An Euler Brick is just a cuboid, or a rectangular box, in which all of the edges (length, depth, and height) have integer dimensions; and in which the diagonals on all three sides are also integers.

 

 

 

 

 

 

So if the length, depth and height are a, b, and c respectively, then a, b, and c are integers, as are the quantities √(a²+b²) and √(b²+c²) and √(c²+a²).

The problem is to find a four dimensional Euler Brick, in which the four sides a, b, c, and d are integers, as are the six face diagonals √(a²+b²) and √(a²+c²) and √(a²+d²) and √(b²+c²) and √(b²+d²) and √(c²+d²), or prove that such a cuboid cannot exist .

 

For further information, please see:

[1] http://www.christianboyer.com/eulerbricks/

[2] http://en.wikipedia.org/wiki/Euler_brick

[3] http://f2.org/maths/peb.html

 

 

You can check for contributions to this problem on the solutions page.

 

——————————–-

This web site developed and maintained by

Tim S Roberts

Email: timro21@gmail.com